Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Make a hole in the middle of a polygon
ResourceFunction["PerforatePolygons"][gr] creates a hole in the middle of each polygon in the 3D graphics gr. | |
ResourceFunction["PerforatePolygons"][gr,r] create a hole of size r, where r is the ratio of the hole size to the polygon size. | |
ResourceFunction["PerforatePolygons"][gr,"type"] decomposes into polygons of the specified "type" before creating holes. |
| "Simple" | simple polygons | |
| "Convex" | convex polygons | |
| "Triangle" | triangles |
A set of polygons:
| In[1]:= |
| Out[1]= | 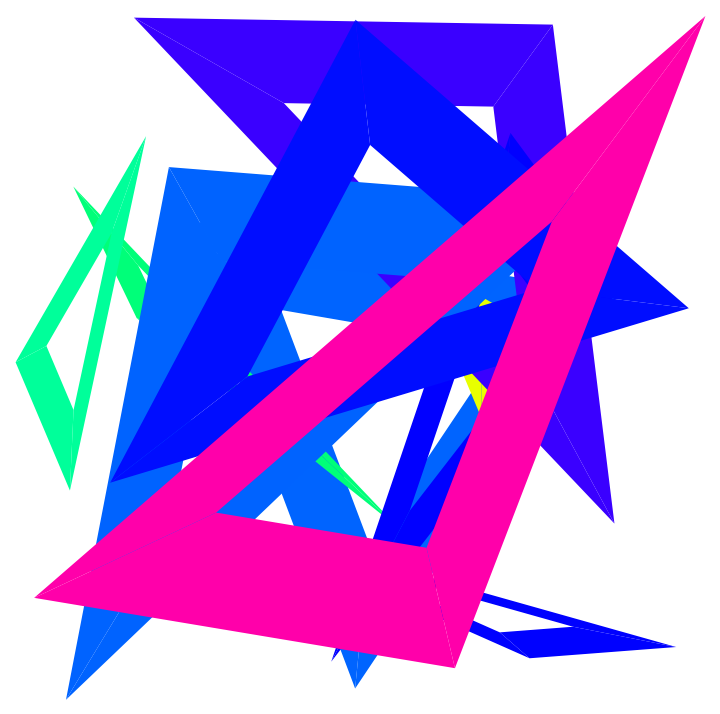 |
Random polygons:
| In[2]:= | ![Graphics[Table[{EdgeForm[Black], Opacity[.5], Hue[RandomReal[]], RandomPolygon[spec]}, {spec, {"Convex", "Simple", "StarShaped", "ConvexHull", 2 -> 10}}]] // ResourceFunction[
"PerforatePolygons"]](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/788414b0dd07951c.png) |
| Out[2]= |  |
A polyhedron:
| In[3]:= |
| Out[3]= | 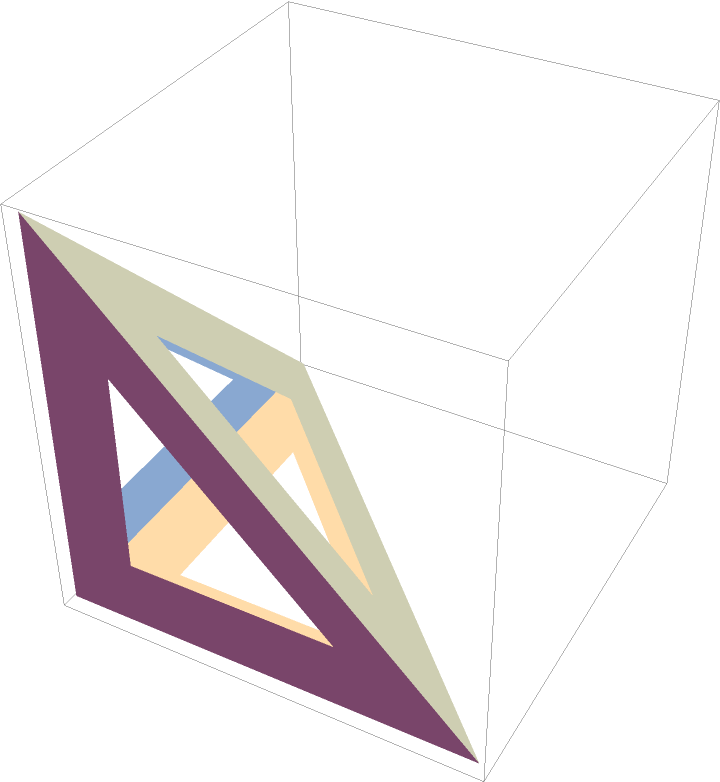 |
| In[4]:= |
| Out[4]= | 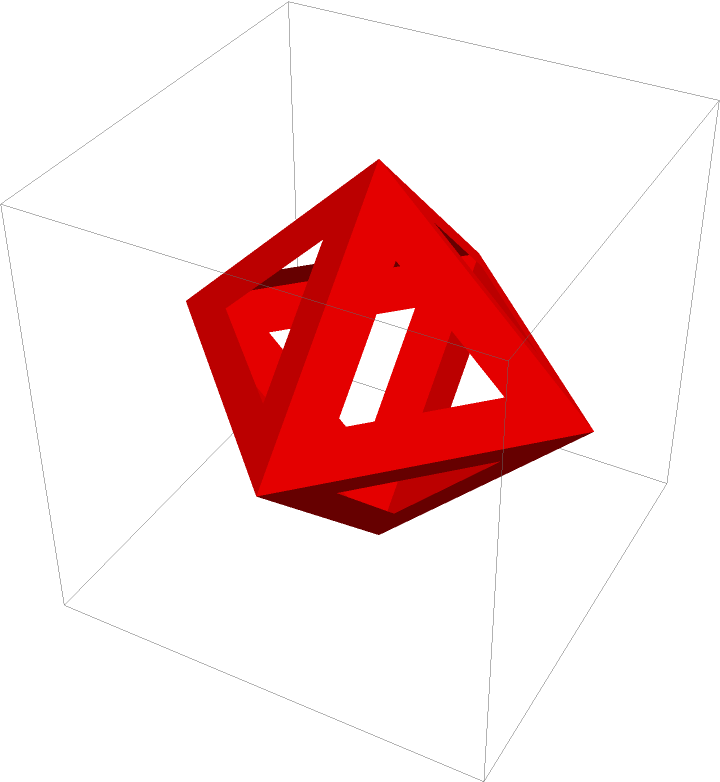 |
Another polyhedron:
| In[5]:= |
| Out[5]= | 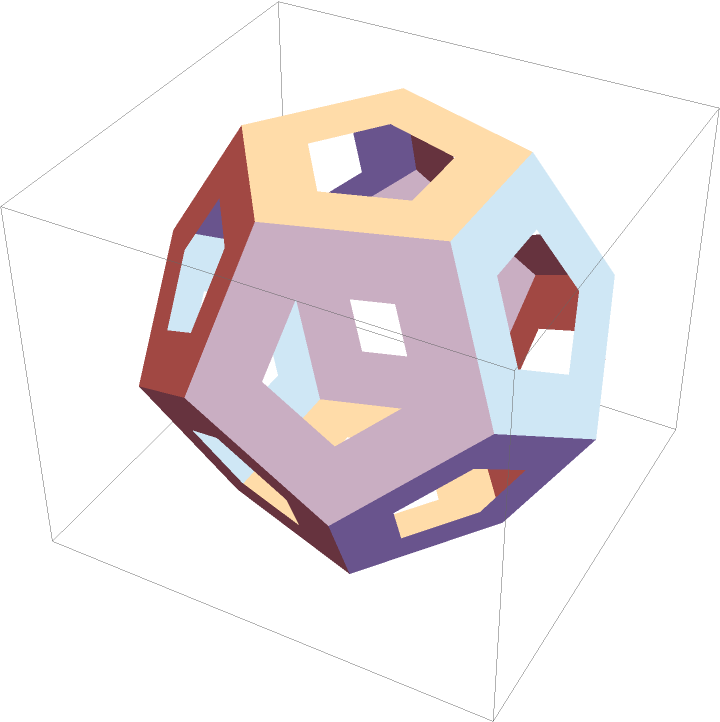 |
Make smaller holes:
| In[6]:= |
| Out[6]= | 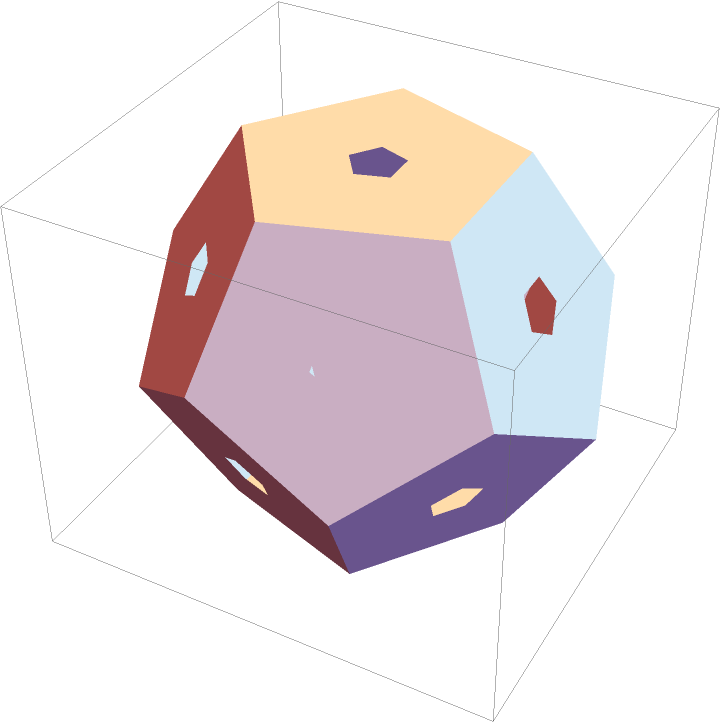 |
With offsets:
| In[7]:= | ![ResourceFunction["PerforatePolygons"][
Graphics[Polygon[{Offset[{10, 10}, {0, 0}], Offset[{0, -20}, {.5, 1}], Offset[{-10, 10}, {1, 0}]}], Frame -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/1e7547c139518fe3.png) |
| Out[7]= | 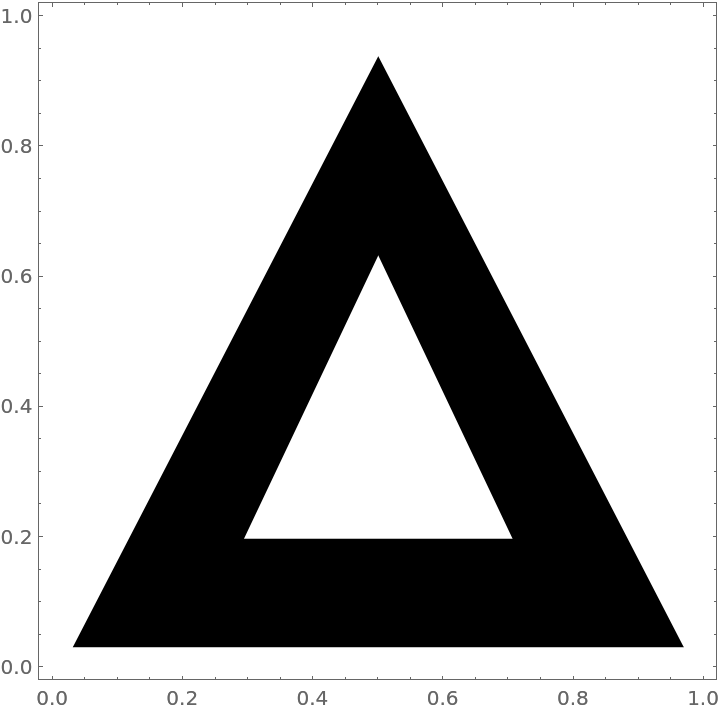 |
With Scaled:
| In[8]:= |
| Out[8]= | 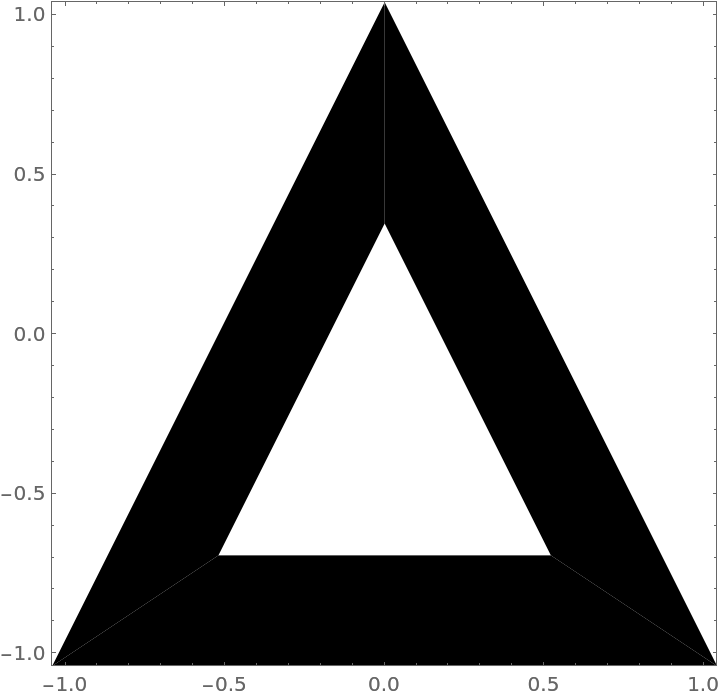 |
With ImageScaled:
| In[9]:= |
| Out[9]= | 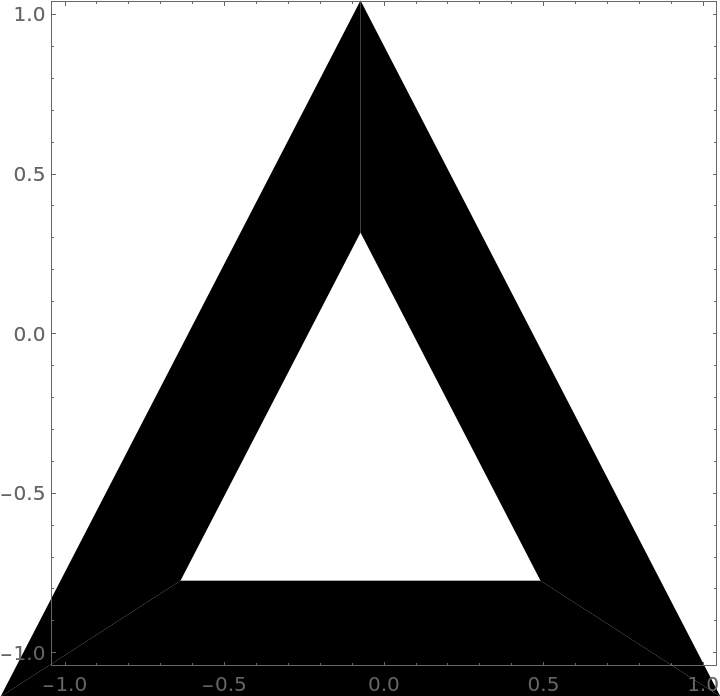 |
A square with a hole with another square inside:
| In[10]:= | ![ResourceFunction["PerforatePolygons"][
Graphics[{EdgeForm[Blue], FaceForm[Pink], Polygon[{{-0.7778174593052023, -0.7778174593052023}, {-0.7778174593052023, 0.7778174593052023}, {-0.5185449728701348, -0.5185449728701348}, {-0.5185449728701348, 0.5185449728701348}, {-0.2592724864350674, -0.2592724864350674}, {-0.2592724864350674, 0.2592724864350674}, {
0.2592724864350674, -0.2592724864350674}, {0.2592724864350674, 0.2592724864350674}, {0.5185449728701348, -0.5185449728701348}, {
0.5185449728701348, 0.5185449728701348}, {
0.7778174593052023, -0.7778174593052023}, {0.7778174593052023, 0.7778174593052023}}, {{1, 11, 12, 2} -> {{4, 10, 9, 3}}, {5, 7, 8, 6}}]}], 0.5]](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/3ac3482638df7647.png) |
| Out[10]= |  |
Sometimes different triangulations can be produced:
| In[11]:= | ![ResourceFunction["PerforatePolygons"][
Graphics[{EdgeForm[Blue], FaceForm[Pink], Polygon[{{-0.7778174593052023, -0.7778174593052023}, {-0.7778174593052023, 0.7778174593052023}, {-0.5185449728701348, -0.5185449728701348}, {-0.5185449728701348, 0.5185449728701348}, {-0.2592724864350674, -0.2592724864350674}, {-0.2592724864350674, 0.2592724864350674}, {
0.2592724864350674, -0.2592724864350674}, {0.2592724864350674, 0.2592724864350674}, {
0.5185449728701348, -0.5185449728701348}, {0.5185449728701348, 0.5185449728701348}, {
0.7778174593052023, -0.7778174593052023}, {0.7778174593052023, 0.7778174593052023}}, {{1, 11, 12, 2} -> {{4, 10, 9, 3}}, {5, 7, 8, 6}}]}], 0.5, #1] & /@ {"Simple", "Convex", "Triangle"} /. EdgeForm[] -> EdgeForm[Blue]](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/2af8fc634f9aa23f.png) |
| Out[11]= |  |
PolygonDecomposition can be used:
| In[12]:= | ![Graphics[{EdgeForm[Blue], FaceForm[Pink], Opacity[.5], ResourceFunction["PerforatePolygons"][
PolygonDecomposition[
Polygon[{{0, 0}, {3, 0}, {3, 1}, {1, 1}, {1, 2}, {3, 2}, {3, 3}, {0, 3}}], #], .5, #]}] & /@ {"Simple", "Convex", "Triangle"} /. EdgeForm[] -> EdgeForm[Blue]](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/42c670534a6c48da.png) |
| Out[12]= |  |
Starting with a polygon with holes:
| In[13]:= | ![Graphics[ResourceFunction["PerforatePolygons"][
Polygon[{{0.25108506944444453`, 0.8149088541666664}, {
1.190776909722223, 0.5390624999999996}, {0.4268337673611113, 0.16174045138888848`}} -> {{{0.3488715277777778, 0.7177191840277776}, {0.3855902777777778, 0.537749565972222}, {
0.5593532986111113, 0.6467339409722221}, {0.3475043402777778, 0.7208984374999999}}, {{0.4085394965277779, 0.40024956597222205`}, {0.49185112847222234`, 0.26394314236111094`}, {0.692621527777778, 0.41199001736111096`}, {0.4085394965277779, 0.40024956597222205`}}, {{0.7003472222222223, 0.5671766493055554}, {1.0040581597222225`, 0.5478407118055555}, {
0.8719835069444446, 0.4357747395833331}, {0.7003472222222223, 0.5671766493055554}}, {{0.5546223958333335, 0.5832682291666667}, {0.45919053819444455`, 0.47585720486111116`}, {0.7017578125000001, 0.47488064236111094`}, {0.5561089409722223, 0.5842773437499998}}}]]] /. Polygon[p_, rest___] :> Scale[Polygon[p, rest], .9]](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/7c653adea69984eb.png) |
| Out[13]= |  |
Using entities:
| In[14]:= |
| Out[14]= |  |
A Bohemian dome surface modifying the ratio of perforation:
| In[15]:= |
| In[16]:= | ![ResourceFunction["PerforatePolygons"][
ParametricPlot3D[
Evaluate[bohdom[1, 1, 1][u, v]], {u, -\[Pi], \[Pi]}, {v, -\[Pi], \[Pi]}, Axes -> None, PlotStyle -> Directive[Orange, Specularity[White, 30]], Mesh -> None, PlotPoints -> 18, MaxRecursion -> 0, Boxed -> False], .7]](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/27995986741d0f2e.png) |
| Out[16]= | 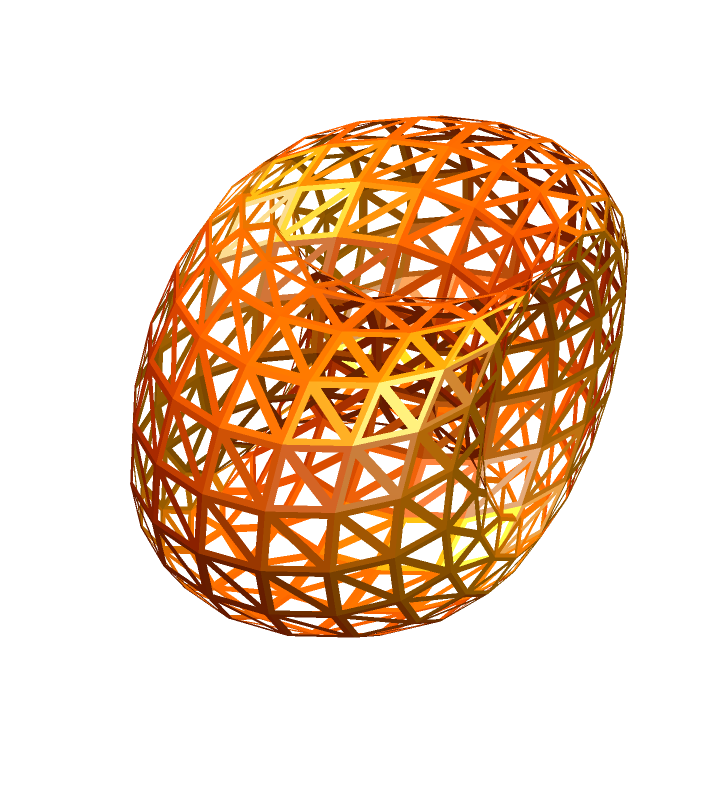 |
PerforatePolygons works with other primitives:
| In[17]:= |
| Out[17]= | 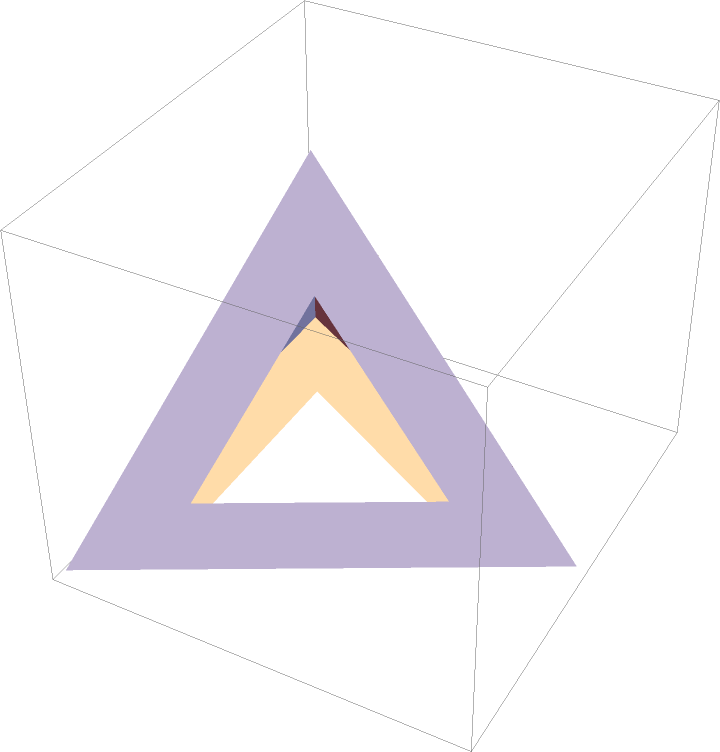 |
Convert into a region:
| In[18]:= |
| Out[18]= | 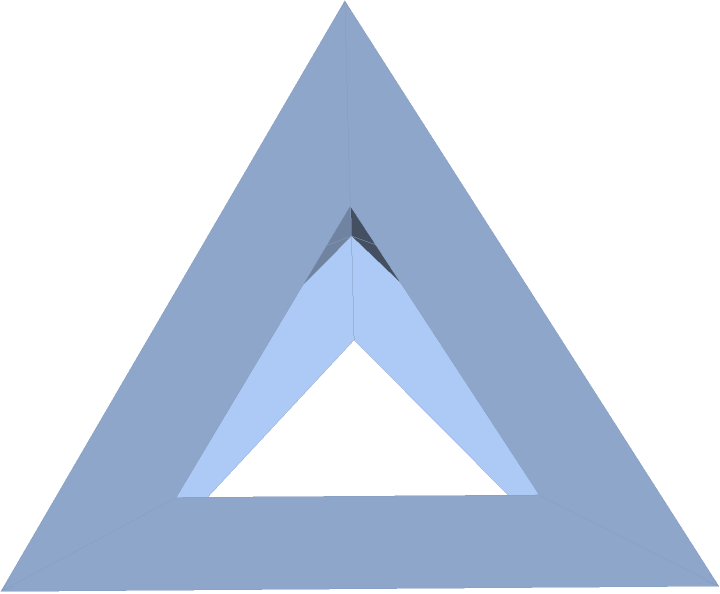 |
Using VertexTextureCoordinates:
| In[19]:= |  |
| In[20]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/eb6dcb1e-a3d3-454c-9213-977d0f0a280b"]](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/4f3313779960e1d2.png) |
| Out[20]= |  |
With VertexColors:
| In[21]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/aa264bfc-9419-415c-bf59-9e0bab16a403"]](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/72d9bf63cc3c2e0a.png) |
| Out[21]= |  |
Disconnected polyhedra:
| In[22]:= | ![ResourceFunction["PerforatePolygons"][
Graphics3D[
Polyhedron[{{0, 0, 0}, {1, 0, 0}, {0, 1, 0}, {0, 0, 1}, {1, 1, 1}, {2, 1, 1}, {1, 2, 1}, {1, 1, 2}}, {{{1, 2, 3}, {1, 2, 4}, {2, 3, 4}, {1, 3, 4}}, {{5, 6, 7}, {5, 6, 8}, {6, 7, 8}, {5, 7, 8}}}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/71b927f6d9f8ee7d.png) |
| Out[22]= | 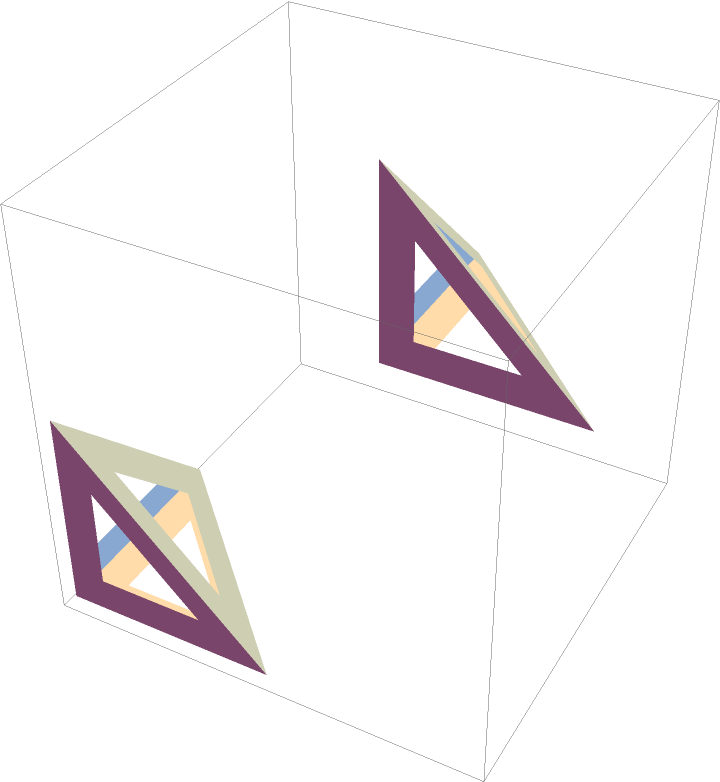 |
A polyhedron with a void:
| In[23]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/d78e3d4d-74de-4c35-b657-467935d847dd"]](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/100a1112dc7961dc.png) |
| Out[23]= | 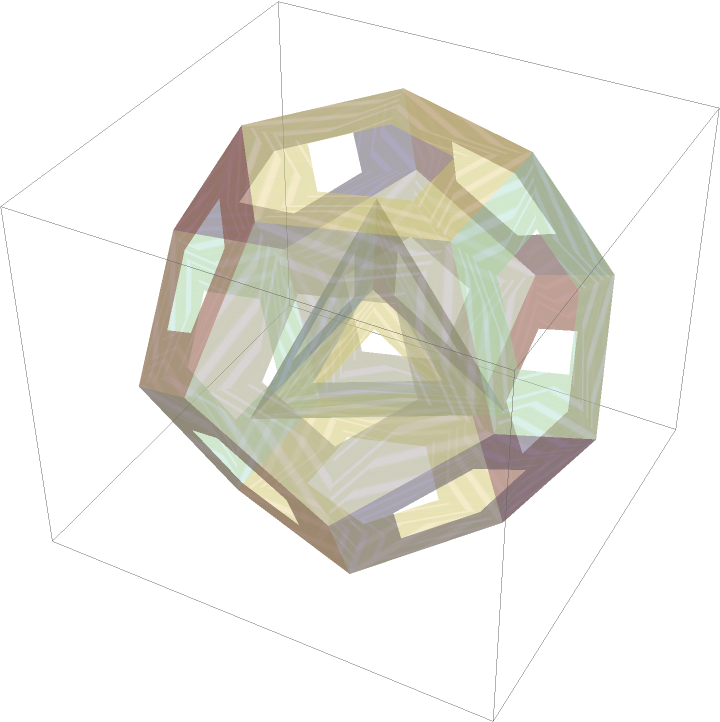 |
A non-convex polyhedron:
| In[24]:= |
| Out[24]= | 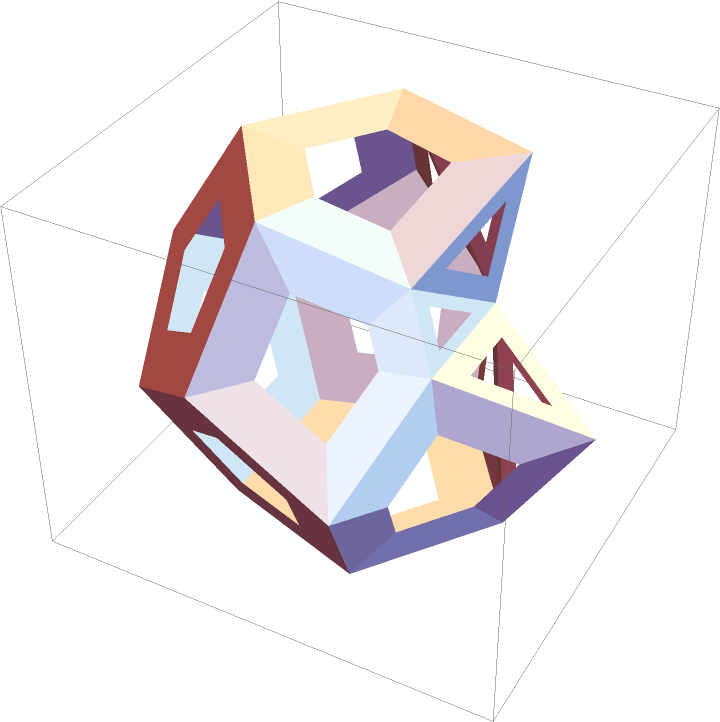 |
A polyhedron with scaled coordinates:
| In[25]:= | ![sp = Polyhedron[
Map[Scaled, {{{0.2, 0., 0.3}, {0.2, 0.9, 0.3}, {1, 0.5, 0.3}}, {{0.2, 0.9, 0.3}, {0.2, 0., 0.3}, {0.5, 0.5, 1.}}, {{1, 0.5, 0.3}, {0.5, 0.5, 1.}, {0.2, 0., 0.3}}, {{0.5, 0.5, 1.}, {1, 0.5, 0.3}, {0.2, 0.9, 0.3}}}, {2}]];](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/650f6f0b8889bf54.png) |
| In[26]:= |
| Out[26]= | 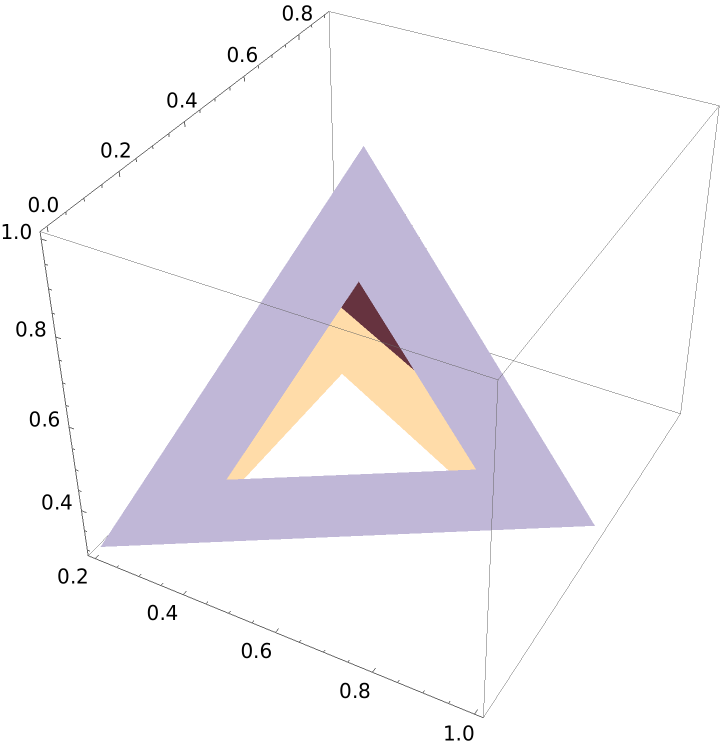 |
A polyhedron with VertexNormals:
| In[27]:= |
| In[28]:= | ![Graphics3D[{Yellow, Polyhedron[{{0, 0, Sqrt[2/3] - 1/(2*Sqrt[6])}, {-1/(2*Sqrt[3]), -1/
2, -1/(2*Sqrt[6])}, {-1/(2*Sqrt[3]), 1/2, -1/(2*Sqrt[6])}, {1/Sqrt[3], 0, -1/(2*Sqrt[6])}}, {{2, 3, 4}, {3, 2, 1}, {4, 1, 2}, {1, 4, 3}}, VertexNormals -> {-n, n, n, n}]}] // ResourceFunction[
"PerforatePolygons"]](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/2aa46d32d24f106c.png) |
| Out[28]= | 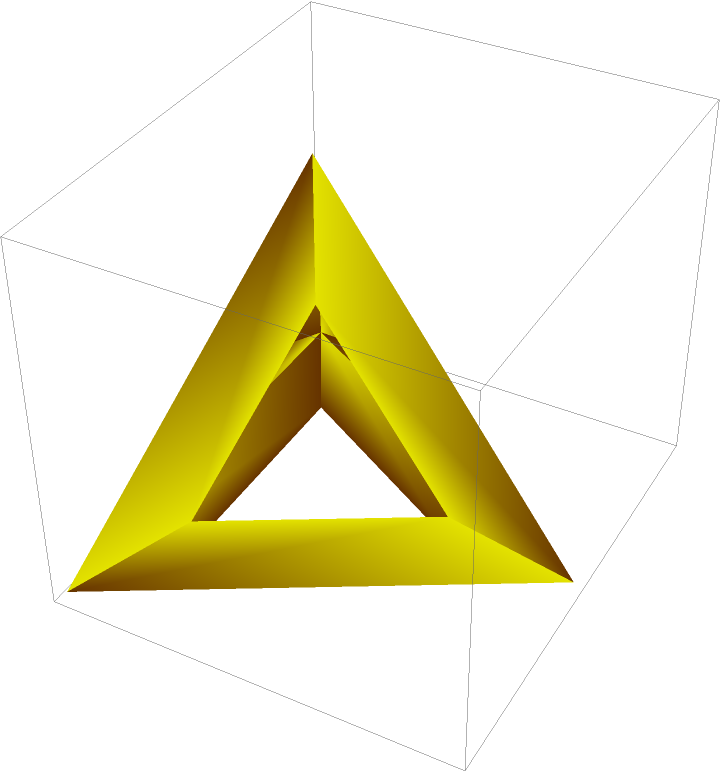 |
A holed hexagonal grid:
| In[29]:= | ![h[x_, y_] := Polygon[Table[
With[{c1 = .25 Cos[(2 \[Pi] k)/6] + x, c2 = .25 Sin[(2 \[Pi] k)/6] + y}, {c1, c2, .5 Sin[.25 c1 c2]}], {k, 7}]]](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/687afd1b41ef6304.png) |
| In[30]:= | ![Graphics3D[{Yellow, Table[h[3 i + 3/(4 4) ((-1)^(4 j) + 1), (Sqrt[3] j)/2], {i, 1, 3, 1/4}, {j, 1, 6, 1/4}]}, Boxed -> False, Background -> Black, SphericalRegion -> True] // ResourceFunction["PerforatePolygons"]](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/4abd15154b886a59.png) |
| Out[30]= |  |
Perforate a prism:
| In[31]:= | ![uehp = ResourceFunction["PerforatePolygons"][
Entity["Polyhedron", {"Prism", 6}]["Graphics3D"]]](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/7dc8058fcb65eeab.png) |
| Out[31]= |  |
Outline the prism:
| In[32]:= |
| Out[32]= |  |
Convert polygons to tubes and vertices to spheres:
| In[33]:= |
| In[34]:= |
| Out[34]= | 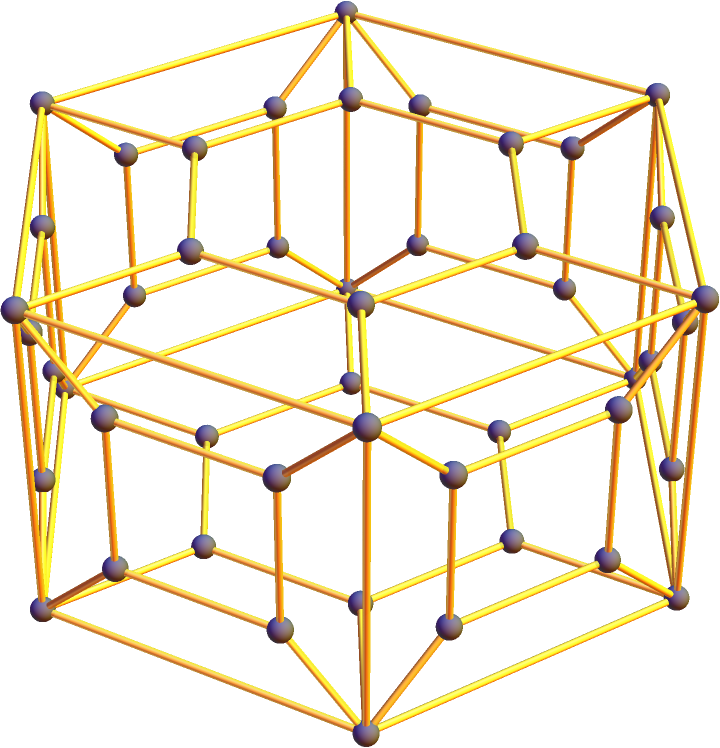 |
Nest perforations:
| In[35]:= | ![Nest[ResourceFunction["PerforatePolygons"], Graphics3D[
Polygon /@ {{{1, 1, 1}, {0, 1, 1}, {0, 0, 1}, {1, 0, 1}}, {{1, 1, 1}, {1, 0, 1}, {1, 0, 0}, {1, 1, 0}}, {{1, 1, 1}, {1, 1, 0}, {0,
1, 0}, {0, 1, 1}}, {{0, 1, 1}, {0, 1, 0}, {0, 0, 0}, {0, 0, 1}}, {{0, 0, 0}, {0, 1, 0}, {1, 1, 0}, {1, 0, 0}}, {{0, 0, 1}, {0, 0, 0}, {1, 0, 0}, {1, 0, 1}}}, Boxed -> False], 5]](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/0464e17f54c021a1.png) |
| Out[35]= |  |
In 3D, if the vertices are not in a plane, the polygon triangulation can be unpredictable:
| In[36]:= |
| Out[36]= | 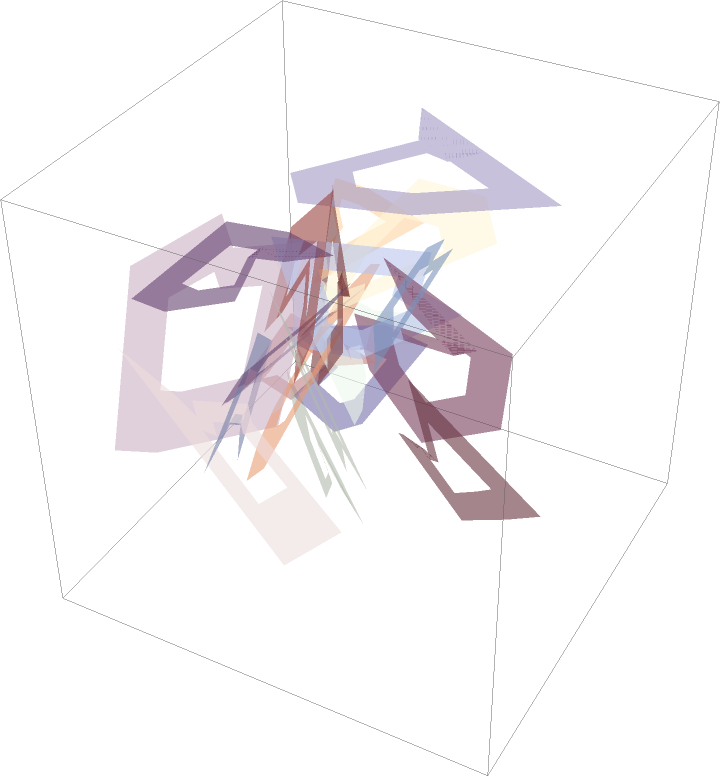 |
Beethoven missing his ninth:
| In[37]:= |
| Out[37]= |  |
A random winding polygon (this may take several minutes):
| In[38]:= |
| In[39]:= | ![Graphics[(Append[#1, VertexColors -> Table[RandomColor[], {Length[#1[[1]]]}]] &) /@ Flatten[Last /@ Most@(ResourceFunction["PerforatePolygons"][
WindingPolygon[RandomReal[1, {200, 2}]], .5])]]](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/72efa1809b4736b4.png) |
| Out[40]= |  |
Decomposing random polygons and perforating twice:
| In[41]:= | ![Map[Graphics[(Append[#1, VertexColors -> Table[RandomColor[], {Length[#1[[1]]]}]] &) /@
DeleteCases[
Flatten@ResourceFunction["PerforatePolygons"][
ResourceFunction["PerforatePolygons"][
Flatten[RandomPolygon[{#, 150}]], #], "Simple"], EdgeForm[], \[Infinity]]] &, {"Simple", "Convex", "ConvexHull", "StarShaped"}] // GraphicsRow](https://www.wolframcloud.com/obj/resourcesystem/images/df2/df293bbe-4677-425b-accd-2d93a22ef955/7d0529a5bc4e26f7.png) |
| Out[41]= | 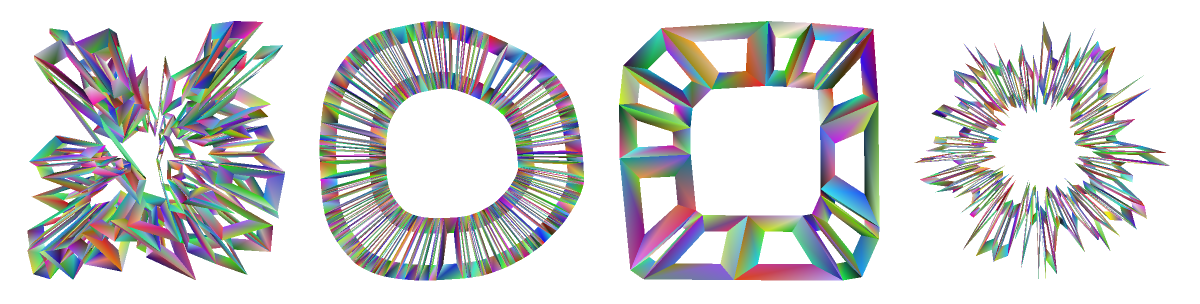 |
This work is licensed under a Creative Commons Attribution 4.0 International License